Алгоритм Зворотного Поширення Помилки

У цій статті я спробую пояснити доступно й українською мовою ключовий алгоритм, що й дозволив увесь сучасний прогрес в області машинного навчання та штучного інтелекту — алгоритм зворотного поширення помилки (з англ. Backpropagation algorithm). Перш, ніж переходити до конкретних кроків та сенсу алгоритму, розберемося, для чого застосовують цей алгоритм.

Алгоритм зворотного поширення помилки, він же backprop, застосовується саме для процесу навчання штучних нейронних мереж і є надзвичайно ефективним для цього. Це навчання штучних нейронних мереж та інших параметризованих функцій (далі називатимемо це просто моделлю) є насправді просто чисельним пошуком параметрів, за яких наша модель помиляється найменше або не помиляється взагалі.

1. Назва й сенс
2. Позначення та матричний запис
3. Функція втрат (витрат)
4. Основні рівняння та принципи
5. Накреси доведень
6. Алгоритм
7. Підсумки й спрощена інтерпретація
8. Завдання

У нас є моделі, що навчаються виконувати якусь задачу автоматично \(\rightarrow\) ми навчаємо їх за допомогою такого математичного об'єкту як градієнт \(\rightarrow\) використовуємо наш надзвичайно ефективний алгоритм backprop, щоб швидко порахувати градієнт. Себто, весь алгоритм — швидкий спосіб порахувати градієнти.

УВАГА: Раджу читати цю статтю лише після прочитання попередньої. Я припускатиму, що ви знаєте, про градієнтний спуск та конструкцію штучної нейронної мережі.

Назва й сенс

Швиденько розберемося з назвою та мотивацією алгоритму. Згадаймо спосіб порахувати похідні та градієнти чисельно зі вступної нотатки про машинне навчання, цей спосіб спирається лише на визначення та непогано наближує похідні. Беремо собі спокійно визначення похідної для \(L'(W) = \underset{h \rightarrow 0}{\lim} \frac{L(W+h) - L(W)}{h}\), підставляємо достатньо малі значення \(h\) та приблизно отримуємо шукане значення. Проблема з цим у тому, що це працює для функцій однієї змінної, а для градієнтного спуску ми маємо порахувати саме градієнт від функції, що залежить від УСІХ параметрів моделі, яких потенційно буде багато. Градієнт (як узагальнення похідної) складається з похідних за ВСІМА аргументами функції (тобто доведеться рахувати дуже багато таких дробів). Отже, такий метод доволі неефективний.

Позначення та матричний запис

Для зручного пояснення алгоритму зворотного поширення помилки нам доведеться ввести певні допоміжні та, як вам здаватиметься на початку, трохи дивні позначення. Утім, це дозволить записати відповідні формули в найкоротшому вигляді. Ми розглядатимемо штучну нейронну мережу з \(N\) шарів. Кожен шар матиме певну кількість нейронів, можливо різну (її позначатимемо по-різному, вона може бути довільна). Позначимо \(\textcolor{coral}{w}^l_{jk}\) вагу (певний числовий множник) переходу сигналу від \(k\)-того нейрону \((l-1)\)-го шару до \(j\)-того нейрону \(l\)-того шару (що більше це число, то більше \(k\)-тий нейрон \((l-1)\)-го шару впливатиме на \(j\)-тий нейрон \(l\)-того шару). Зверніть увагу, що \(l\) в \(\textcolor{coral}{w}^l_{jk}\) — не степінь, а верхній індекс (просто позначка для нумерації). Аналогічним чином позначатимемо параметр зміщення на \(j\)-тому нейроні \(l\)-того шару \(\textcolor{steelblue}{b}^l_j\).

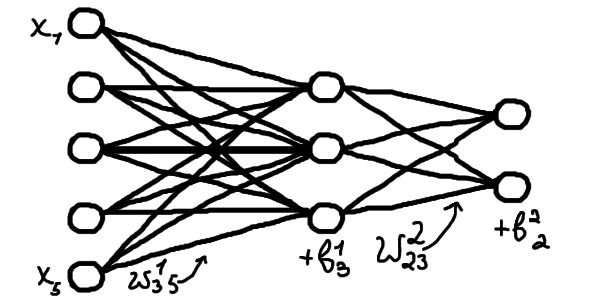
Активований сигнал \(\textcolor{firebrick}{a}^l_j\) на \(j\)-тому нейроні \(l\)-того шару виражається через значення на нейронах попереднього \((l-1)\)-го шару наступним чином \[\textcolor{firebrick}{a}^l_j = \textcolor{mediumseagreen}{\sigma(} \textcolor{coral}{w}^l_{j1}\textcolor{firebrick}{a}^{l-1}_1 + \textcolor{coral}{w}^l_{j2}\textcolor{firebrick}{a}^{l-1}_2 + ... + \textcolor{coral}{w}^l_{jk}\textcolor{firebrick}{a}^{l-1}_k + \textcolor{steelblue}{b}^l_j\textcolor{mediumseagreen}{)} \tag{1} \] де \(\textcolor{mediumseagreen}{\sigma(\textcolor{black}{\cdot})}\) — нелінійна функція активації. Функцію активації загалом обирають різну (головне нелінійну), однак позначення літерою "сигма" я вибрав через дуже розповсюджену в контексті нашого алгоритму функцію, що називається сигмоїдою: \(\textcolor{mediumseagreen}{\sigma(\textcolor{black}{x})} = e^x/(e^x+1)\). Можете уявляти тут саме цю функцію, можете якусь іншу, якщо вже мали досвід із нею як із функцією активації.

Неактивований сигнал відповідного нейрону (тобто той самий вираз, але без функції активації) позначимо як \(\textcolor{indianred}{p}^l_j\): \[\textcolor{indianred}{p}^l_j = \textcolor{coral}{w}^l_{j1}\textcolor{firebrick}{a}^{l-1}_1 + \textcolor{coral}{w}^l_{j2}\textcolor{firebrick}{a}^{l-1}_2 + ... + \textcolor{coral}{w}^l_{jk}\textcolor{firebrick}{a}^{l-1}_k + \textcolor{steelblue}{b}^l_j,\] \[\textcolor{firebrick}{a}^l_j = \textcolor{mediumseagreen}{\sigma(}\textcolor{indianred}{p}^l_j \textcolor{mediumseagreen}{)} \tag{1.1}\]

Також можемо переписати верхнє рівняння в матрично-векторному вигляді для скорочення та спрощення. Щоб у такому вигляді ми могли використовувати нашу числову функцію активації \(\textcolor{mediumseagreen}{\sigma(}\cdot\textcolor{mediumseagreen}{)}\), розглядатимемо узагальнення цієї функції для векторів/масивів наступним чином: \( \textcolor{mediumseagreen}{ \boldsymbol{\sigma} \left( \textcolor{black}{\left[ \begin{array}{c} x_0 \\ x_1 \end{array} \right] } \right) } = \left[ \begin{array}{c} \textcolor{mediumseagreen}{\sigma(}x_0\textcolor{mediumseagreen}{)} \\ \textcolor{mediumseagreen}{\sigma(}x_1\textcolor{mediumseagreen}{)} \end{array} \right]\). Тобто коли ми записуємо числову функцію й підставляємо векторний чи матричний аргумент, то мається на увазі просто вектор/матриця, де ми застосували цю числову функцію до кожного аргументу окремо. Таким чином, рівняння (1) узагальнюється для всього шару \(l\) як \[ \textcolor{firebrick}{\boldsymbol{a}}^l = \textcolor{mediumseagreen}{\boldsymbol{\sigma}(} \textcolor{coral}{W}^l\textcolor{firebrick}{\boldsymbol{a}}^{l-1} + \textcolor{steelblue}{\boldsymbol{b}}^l\textcolor{mediumseagreen}{)} \tag{1.2} \] де \(\textcolor{mediumseagreen}{\sigma(}\cdot\textcolor{mediumseagreen}{)}\) — нелінійна функція активації; \(\textcolor{coral}{W}^l\) — матриця вагів усіх нейронів шару \(l\); \(\textcolor{firebrick}{\boldsymbol{a}}^l\) — вектор з усіх активованих значень нейронів шару \(l\); \(\textcolor{steelblue}{\boldsymbol{b}}^l\) — вектор з параметрів зміщення всіх нейронів шару \(l\).

Введемо також операцію по-елементного множення векторів для спрощення певних записів: \[\left(\begin{array}{c} 1 \\ 2 \end{array}\right) \odot \left(\begin{array}{c} 3 \\ 4\end{array} \right) = \left( \begin{array}{c} 1 \cdot 3 \\ 2 \cdot 4 \end{array} \right) = \left( \begin{array}{c} 3 \\ 8 \end{array} \right)\] Зверніть увагу, ця операція не має прямого стосунку до скалярного, векторного, зовнішнього та інших добутків векторів, що розглядаються в лінійній алгебрі. Це просто множення всіх елементів одного вектора на інший як зручний спосіб записувати певні вирази.

Функція втрат (витрат)

У попередній нотатці ми вже побачили, як оцінювати помилку нейронної мережі за певних параметрів та назвали це функцією втрат \(\textcolor{darkcyan}{L}\). Та функція називалася середнє абсолютне відхилення. Тут ми визначимо й позначимо її трохи по-іншому, а саме оберемо функцію середнього квадратичного відхилення як оцінку похибки: \[\textcolor{darkcyan}{L} = \frac{1}{2\textcolor{orangered}{k}}\left(||\boldsymbol{y}_\textcolor{orangered}{1} - \textcolor{firebrick}{\boldsymbol{a}}^N\textcolor{firebrick}{(}\boldsymbol{x}_\textcolor{orangered}{1}\textcolor{firebrick}{)}||^2 + ||\boldsymbol{y}_\textcolor{orangered}{2} - \textcolor{firebrick}{\boldsymbol{a}}^N\textcolor{firebrick}{(}\boldsymbol{x}_\textcolor{orangered}{2}\textcolor{firebrick}{)}||^2 + ... + ||\boldsymbol{y}_\textcolor{orangered}{k} - \textcolor{firebrick}{\boldsymbol{a}}^N\textcolor{firebrick}{(}\boldsymbol{x}_\textcolor{orangered}{k}\textcolor{firebrick}{)}||^2 \right) \tag{2}\] де \(\textcolor{firebrick}{\boldsymbol{a}}^N\textcolor{firebrick}{(}\boldsymbol{x}_i\textcolor{firebrick}{)}\) — значення останнього \(N\)-того шару мережі за вхідного вектору \(\boldsymbol{x}_i\), тобто те, що видала модель на \(i\)-тому тренувальному прикладі; \(\boldsymbol{y}_i\) — правильний результат на \(i\)-тому тренувальному прикладі; \(\textcolor{orangered}{k}\) — кількість тренувальних прикладів у наборі даних.

Ця величина \(\textcolor{darkcyan}{L}\) показує, наскільки загалом відхиляється модель, бо вона дорівнює середньому значенню з різниць між тим, що видала модель \(\textcolor{firebrick}{\boldsymbol{a}}^N\textcolor{firebrick}{(}\boldsymbol{x}_i\textcolor{firebrick}{)}\), та тим, що ми хотіли б від неї отримати \(\boldsymbol{y}_i\), на всіх тренувальних прикладах. Правда, ми беремо не просто ці різниці, а їх у квадраті, щоб "підсилити ефект" та додатково ділимо все значення на 2. Якщо прибрати квадрати та \(\frac{1}{2}\), то вийде вже відома нам функція втрат (середнє абсолютне відхилення). Алгоритм зворотного поширення помилки можна застосувати до обох цих функцій, але ми скористаємося квадратичним варіянтом \((2)\).

А в яких випадках узагалі застосовний алгоритм зворотного поширення помилки? Загалом, є лише дві умови на функцію втрат, виконання яких ми вимагаємо. Перша: функцію втрат можна записати як середнє з втрат на окремих прикладах, тобто \[\textcolor{darkcyan}{L} = \frac{1}{k} \left( \textcolor{darkcyan}{\mathfrak{L}}_{\boldsymbol{x}_1} + ... + \textcolor{darkcyan}{\mathfrak{L}}_{\boldsymbol{x}_k} \right) \tag{2.1}\] де \(\textcolor{darkcyan}{\mathfrak{L}}_{\boldsymbol{x}_i}\) — окрема похибка на одному \(i\)-тому прикладі, а \(\textcolor{darkcyan}{L}\) — загальна функція похибки. Це в нас, очевидно, виконується, бо ми саме так і визначали функцію втрат.

Навіщо така умова? Згадаємо, що в результаті алгоритм має знайти градієнт функції втрат (нагадування, що таке градієнт), \(\nabla \textcolor{darkcyan}{L}\), за поточних параметрів \(\textcolor{coral}{W}\) та \(\textcolor{steelblue}{\boldsymbol{b}}\). Градієнт складається з похідних за всіма параметрами, тобто з \(\partial \textcolor{darkcyan}{L} /\partial \textcolor{coral}{W}\) та \(\partial \textcolor{darkcyan}{L} /\partial \textcolor{steelblue}{\boldsymbol{b}}\). Ця перша умова потрібна саме тому, що backprop буде знаходити похідні \(\partial \textcolor{darkcyan}{\mathfrak{L}}_{\boldsymbol{x}_i} /\partial \textcolor{coral}{W}\) та \(\partial \textcolor{darkcyan}{\mathfrak{L}}_{\boldsymbol{x}_i} /\partial \textcolor{steelblue}{\boldsymbol{b}}\) саме для окремих похибок \(\textcolor{darkcyan}{\mathfrak{L}}_{\boldsymbol{x}_i}\). Тобто ми зможемо скласти окремі градієнти \(\nabla \textcolor{darkcyan}{\mathfrak{L}}_{\boldsymbol{x}_i}\) і скласти з них шуканий \(\nabla \textcolor{darkcyan}{L}\) усередненням: \[\textcolor{sienna}{\nabla}\textcolor{darkcyan}{L} = \frac{1}{k} \textcolor{sienna}{\nabla}\left( \textcolor{darkcyan}{\mathfrak{L}}_{\boldsymbol{x}_1} + ... + \textcolor{darkcyan}{\mathfrak{L}}_{\boldsymbol{x}_k} \right) = \frac{1}{k} \left( \textcolor{sienna}{\nabla}\textcolor{darkcyan}{\mathfrak{L}}_{\boldsymbol{x}_1} + ... + \textcolor{sienna}{\nabla}\textcolor{darkcyan}{\mathfrak{L}}_{\boldsymbol{x}_k} \right) \tag{2.2}\]

Надалі ми будемо використовувати \(\textcolor{darkcyan}{\mathfrak{L}}\) для позначення похибки моделі на окремому тренувальному прикладі та \(\textcolor{darkcyan}{L}\) для загальної функції втрат (похибки). Ми хочемо, в цілому, мінімізувати як \(\textcolor{darkcyan}{\mathfrak{L}}\), так і \(\textcolor{darkcyan}{L}\).

Друга умова: функція втрат має виражатися через результат роботи моделі \(\textcolor{firebrick}{\boldsymbol{a}}^N\). Це цілком природно, \(\textcolor{darkcyan}{L}\) має бути функцією, що залежить від нашої моделі (тобто її параметрів) та не залежить від якихось зовнішніх факторів. Погляньмо на \((2)\), це справді виконується, бо все в нашому визначенні, крім моделі, буде фіксованим та чітко визначеним: \[\textcolor{darkcyan}{L(}\textcolor{firebrick}{\boldsymbol{a}}^N\textcolor{darkcyan}{)} = \textcolor{lightgrey} {\frac{1}{2k}\left(||\boldsymbol{y}_1 - \textcolor{firebrick}{\boldsymbol{a}}^N\textcolor{firebrick}{(}\boldsymbol{x}_1\textcolor{firebrick}{)}||^2 + ||\boldsymbol{y}_2 - \textcolor{firebrick}{\boldsymbol{a}}^N\textcolor{firebrick}{(}\boldsymbol{x}_2\textcolor{firebrick}{)}||^2 + ... + ||\boldsymbol{y}_k - \textcolor{firebrick}{\boldsymbol{a}}^N\textcolor{firebrick}{(}\boldsymbol{x}_k\textcolor{firebrick}{)}||^2 \right)}\] Трохи поясню, чому ж ми можемо сприймати все інше у виразі праворуч як сталі: кількість прикладів у датасеті \(\textcolor{orangered}{k}\) буде незмінною протягом процесу тренування, бо ми набір даних не змінюється. З тої самої причини незмінними на тренуванні будуть і пари самих тренувальих прикладів \((\boldsymbol{x}_i; \boldsymbol{y}_i)\).

Основні рівняння та принципи

Ми зачепили ключову для сприйняття зворотного поширення помилки річ — частинні похідні. Справді, якщо наша мета — знайти градієнт функції втрат від параметрів \(\nabla \textcolor{darkcyan}{L(\textcolor{coral}{W},\textcolor{steelblue}{\boldsymbol{b}})}\), то нам для цього потрібні частинні похідні \(\partial \textcolor{darkcyan}{L} /\partial \textcolor{coral}{w}\) від функції втрат за всіма окремими параметрами \(\textcolor{coral}{w}\). Ці частинні похідні характеризуватимуть, наскільки змінюється значення \(\textcolor{darkcyan}{L}\) при малих змінах \(\textcolor{coral}{w}\) біля точки, де ми зараз знаходимося. На цій інтуїції ми побудуємо трохи інше бачення навчання градієнтним спуском, не таке, як будували в попередній нотатці, а бачення для кожного окремого нейрона й параметра окремо. Це бачення дозволить далі сприймати backprop простіше.

Пригадаймо формулу для градієнтного спуску (бажано, щоб ви також пригадали іншу інтуїцію щодо неї, про яку ми вже говорили раніше): \[ \textcolor{coral}{W}_{\textcolor{blue}{n}+1} = \textcolor{coral}{W}\textcolor{blue}{_n} - \textcolor{purple}{\alpha} \cdot \nabla \textcolor{darkcyan}{L(\textcolor{coral}{W}\textcolor{blue}{_n})} \tag{3}\] (аналогічно для \(\textcolor{steelblue}{\boldsymbol{b}}\)). Ця формула описує крок градієнтного спуску, тобто виражає новий набір параметрів, \(\textcolor{coral}{W}_{\textcolor{blue}{n}+1}\), після оновлення на цьому кроці через попередній набір параметрів до цього кроку, \(\textcolor{coral}{W}_{\textcolor{blue}{n}}\). Формулу записано для всіх параметрів одочасно, але її можна також сприймати як окремі правила для окремих параметрів, якщо згадати, що градієнт складається з частинних похідних. Тоді вийде, що для окремого параметру \(\textcolor{coral}{w}\) десь усередині моделі, кожен крок градієнтного спуску його буде змінено таким чином: \[ \textcolor{coral}{w}_{\textcolor{blue}{n}+1} = \textcolor{coral}{w}\textcolor{blue}{_n} - \textcolor{purple}{\alpha} \cdot \frac{\partial \textcolor{darkcyan}{L}}{\partial \textcolor{coral}{w}\textcolor{blue}{_n}} \tag{3.1}\] А от як нам інтерпретувати це правило \((3.1)\)? Знову таки, частинні похідні характеризуватимуть, наскільки змінюється значення \(\textcolor{darkcyan}{L}\) при малих змінах \(\textcolor{coral}{w}\) біля точки, де ми зараз знаходимося \(\textcolor{coral}{w}\textcolor{blue}{_n}\). Є два (насправді більше) випадки відношення між зміною \(\textcolor{coral}{w}\) та \(\textcolor{darkcyan}{L}\): \[1) \text{ збільшуємо трохи } \textcolor{coral}{w} \rightarrow \text{ЗБІЛЬШУЄТЬСЯ } \textcolor{darkcyan}{L}\] \[2) \text{ збільшуємо трохи } \textcolor{coral}{w} \rightarrow \text{зменшується } \textcolor{darkcyan}{L}\] Враховуючи, що наша задача — зменшити \(\textcolor{darkcyan}{L}\), бо вона характеризує помилку, в першому випадку нам потрібно трохи зменшити \(\textcolor{coral}{w}\), а в другому — збільшити його. Цим випадкам відповідають додатній та від'ємний знаки похідної \(\partial \textcolor{darkcyan}{L} /\partial \textcolor{coral}{w}\). Отже ми маємо трохи змінити \(\textcolor{coral}{w}\) так, щоб зменшити \(\textcolor{darkcyan}{L}\), тобто в бік \(-\partial \textcolor{darkcyan}{L} /\partial \textcolor{coral}{w}\) на дуже маленьке число (тому обираємо певне мале \(0 < \textcolor{purple}{\alpha} < 1\) як множник).

Ще раз: ми дивимося на окремий параметр в окремому нейроні й за допомогою частинної похідної змінюємо його так, щоб покращити роботу моделі загалом. Тобто коригуємо роботу окремого нейрону. Задача алгоритму зворотного поширення помилки — в найефективніший спосіб установити, як саме змінювати кожен параметр. Виявляється, це можна зробити, якщо обходити нейрони з останніх шарів до перших, тобто в зворотному порядку, звідки й назва алгоритму. Тобто ми будемо для кожного параметру моделі рахувати те, як він упливає на похибку моделі, починаючи з останніх шарів і просуваючись до перших.

Щоправда, виникає проблема в тому, що нейрон має не один параметр, а багато. Якщо попередній шар мав \(m\) нейронів, то кожен нейрон наступного шару в класичній (повнозв'язній) нейронній мережі матиме \(m+1\) параметр: множники \(\textcolor{coral}{w}_1 ... \textcolor{coral}{w}_m\) та зміщення \(\textcolor{steelblue}{b}\) (див. \((1)\)). Отже потрібно розрізняти частинні похідні від функції втрат \(\textcolor{darkcyan}{L}\) за окремими параметрами (тобто як залежить похибка від значення параметру) від того, як залежить похибка \(\textcolor{darkcyan}{L}\) від значення цілого нейрону. Це, звісно, пов'язані величини, але нейрон складається з декількох параметрів. Позначимо це так: \[\frac{\partial \textcolor{darkcyan}{L}}{\partial \textcolor{coral}{w}^l_{jk}}, \frac{\partial \textcolor{darkcyan}{L}}{\partial \textcolor{steelblue}{b}^l_j} \text{ — похибки на окремих параметрах певного шару}\] \[\textcolor{darkcyan}{\delta}^l_j \equiv \frac{\partial \textcolor{darkcyan}{L}}{\partial \textcolor{indianred}{p}^l_j} \text{ — похибка неактивованого значення певного нейрону певного шару} \tag{4}\] Простіше кажучи, \(\textcolor{darkcyan}{\delta}^l_j\) — міра того, наскільки помиляється модель на конкретному \(j\)-тому нейроні \(l\)-того шару.

Надалі, одна з наших задач буде в тому, щоб установити співвідношення між величинами в рівняннях \((4)\), щоб ми й справді могли "просуватися" поступово від передніх шарів до попередніх. Утім, це лише одна з задач, які перед нами постають. Усього в алгоритмі backprop буде чотири рівняння й, мушу зазначити, вони не дуже прості, на них потрібен час і кількаразове перечитування пояснень. Ці рівняння описують повністю, як нам просуватися вглиб мережі, рахуючи всі потрібні похибки/частинні похідні, починаючи при тому з кінця, тобто з самого значення загальної функції втрат \(\textcolor{darkcyan}{L}\), яке ми можемо обрахувати. Також варто зазначити, що так званий зворотний прохід робиться вже після проходу звичайного й намагається максимально використовувати вже відому з прямого проходу інформацію. Себто, прямий прохід рахує відповідь мережі на наші дані, зворотний рахує, як її покращити.

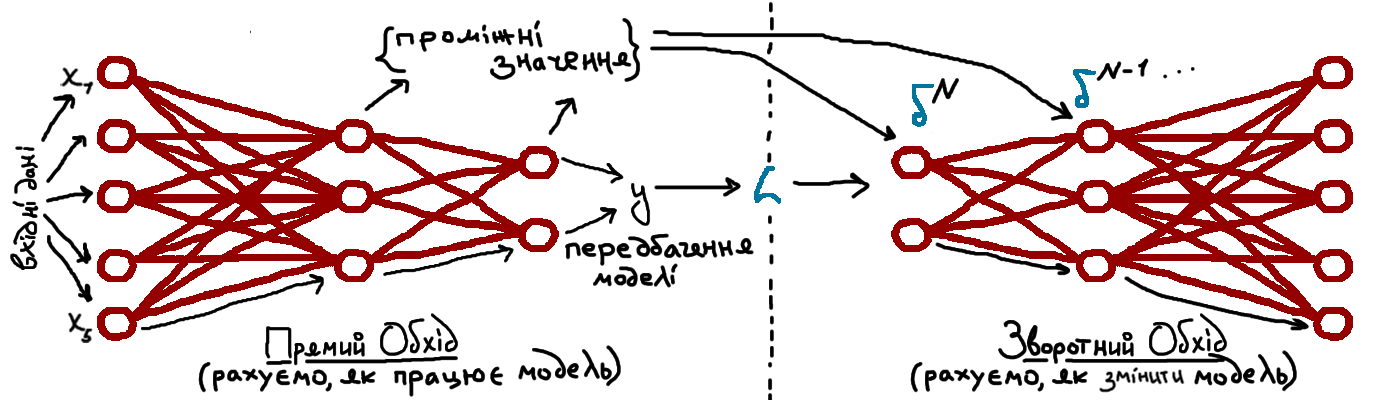
Отже, наведу вам чотири рівняння зворотного поширення помилки з поясненнями. Доведення (точніше, "скетчі" доведень) будуть трохи пізніше.

Рівняння похибок нейронів для останнього, \(N\)-того, шару мережі. \[ \textcolor{darkcyan}{\delta}^N_j = \frac{\partial \textcolor{darkcyan}{L}}{\partial \textcolor{firebrick}{a}^N_j} \cdot \textcolor{mediumseagreen}{\sigma\textcolor{black}{'}(\textcolor{indianred}{p} \textcolor{black}{^N_j})} \tag{backprop 1} \] де \(\frac{\partial \textcolor{darkcyan}{L}}{\partial \textcolor{firebrick}{a}^N_j}\) — похідна від функції втрат за активованим сигналом \(j\)-того нейрону останнього (\(N\)-того) шару; \(\textcolor{mediumseagreen}{\sigma\textcolor{black}{'}(\textcolor{indianred}{p} \textcolor{black}{^N_j})}\) — похідна від функції активації в точці \(\textcolor{indianred}{p} \textcolor{black}{^N_j}\); \(\textcolor{indianred}{p} \textcolor{black}{^N_j}\) — неактивований (лінійний) сигнал з \(j\)-того нейрону останнього (\(N\)-того) шару.

Це рівняння — наш перший крок щодо просування вглиб мережі, тобто спосіб обчислити окремі значення похибки на останньому шарі. Усі величини в правій частині цього рівняння можна легко обчислити: функція активації \(\textcolor{mediumseagreen}{\sigma(\textcolor{black}{\cdot})}\) — просто числова функція, у якої ми знаємо аналітичний вираз для її похідної \(\textcolor{mediumseagreen}{\sigma\textcolor{black}{'}(\textcolor{black}{\cdot})}\), куди підставити обчислене нами значення \(\textcolor{indianred}{p} \textcolor{black}{^N_j}\) буде не дуже складно. Наприклад, для сигмоїди \(\textcolor{mediumseagreen}{\sigma(\textcolor{black}{x})} = e^x/(e^x+1)\) похідна буде виражатися через саму сигмоїду: \(\textcolor{mediumseagreen}{\sigma\textcolor{black}{'}(\textcolor{black}{x})} = \textcolor{mediumseagreen}{\sigma(\textcolor{black}{x})}(1-\textcolor{mediumseagreen}{\sigma(\textcolor{black}{x})})\), що дозволить легко її обчислювати, знаючи значення самої сигмоїди в тій самій точці, а це як правило буде відомо нам із прямого обходу, який ми здійснимо перед зворотним. Похідну \(\partial \textcolor{darkcyan}{L}/\partial \textcolor{firebrick}{a}^N_j\) теж обчислити неважко. Для похибки \(\textcolor{darkcyan}{\mathfrak{L}}\) на кожному окремому прикладі \(\boldsymbol{x}\) з тренувального набору матимемо \[ \frac{\partial}{\partial \textcolor{firebrick}{a}^N_j} \textcolor{darkcyan}{\mathfrak{L}} = \frac{\partial}{\partial \textcolor{firebrick}{a}^N_j} \left[ \frac{1}{2} ||\boldsymbol{y} - \textcolor{firebrick}{\boldsymbol{a}}^N\textcolor{firebrick}{(\textcolor{black}{\boldsymbol{x}})}||^2 \right] = (\textcolor{firebrick}{a}^N_j\textcolor{firebrick}{(\textcolor{black}{\boldsymbol{x}})} - \boldsymbol{y}). \tag{5} \] Відповідно, можемо встановити й \(\partial \textcolor{darkcyan}{L}/\partial \textcolor{firebrick}{a}^N_j\) за допомогою \((5)\) та \((2.2)\).

Для всього останнього шару одночасно \((\text{backprop }1)\) можна переписати як: \[ \textcolor{darkcyan}{\boldsymbol{\delta}}^N = \left( \nabla_{\textcolor{firebrick}{a}^N} \textcolor{darkcyan}{L} \right) \odot \left( \textcolor{mediumseagreen}{\boldsymbol{\sigma}\textcolor{black}{'}(\textcolor{indianred}{\boldsymbol{p}} \textcolor{black}{^N})} \right) \tag{backprop 1.1} \] де \(\nabla_{\textcolor{firebrick}{a}^N} \textcolor{darkcyan}{L}\) — градієнт (вектор похідних) за всіма \(\textcolor{firebrick}{a}^N_j\); \(\textcolor{mediumseagreen}{\sigma\textcolor{black}{'}(\textcolor{black}{\cdot})}\) — похідна від функції активації; \(\textcolor{indianred}{\boldsymbol{p}} \textcolor{black}{^N}\) — вектор неактивованих сигналів нейронів останнього шару. Формула задається поелементним множенням двох векторів однакової розмірности (такої як кількість нейронів останнього шару). Відповідно, кожен окремий елемент \(\textcolor{darkcyan}{\delta}^N_j\) вектору \(\textcolor{darkcyan}{\boldsymbol{\delta}}^N\) відповідає рівнянню \((\text{backprop }1)\). У векторній формі зможемо дуже легко порахувати ці похибки на практиці такими інструментами, наприклад NumPy у Python чи засобами мови Julia.

Рівняння похибки шару, \(\textcolor{darkcyan}{\boldsymbol{\delta}}^l\), через похибку наступного шару мережі, \(\textcolor{darkcyan}{\boldsymbol{\delta}}^{l+1}\). \[ \textcolor{darkcyan}{\boldsymbol{\delta}}^l = \left( \left(\textcolor{coral}{W}^{l+1}\right)^\top \textcolor{darkcyan}{\boldsymbol{\delta}}^{l+1} \right) \odot \left( \textcolor{mediumseagreen}{\boldsymbol{\sigma}\textcolor{black}{'}(\textcolor{indianred}{\boldsymbol{p}} \textcolor{black}{^l})} \right) \tag{backprop 2} \] де \(\left(\textcolor{coral}{W}^{l+1}\right)^\top\) — транспонована (перевернута відносно діягоналі) матриця вагів (параметрів-множників) \((l+1)\)-го шару; \(\textcolor{darkcyan}{\boldsymbol{\delta}}^l\), \(\textcolor{darkcyan}{\boldsymbol{\delta}}^{l+1}\) — похибки відповідних шарів; \(\textcolor{mediumseagreen}{\sigma\textcolor{black}{'}(\textcolor{black}{\cdot})}\) — похідна від функції активації; \(\textcolor{indianred}{\boldsymbol{p}} \textcolor{black}{^l}\) — вектор неактивованих сигналів нейронів \(l\)-того шару.

Маючи таке рівняння, що виражає похибку попереднього шару через похибку наступного та вже відомі нам величини, ми можемо по черзі порахувати похибки ВСІХ шарів, уявляєте? Перший шар рахується за \((\text{backprop }1)\), а далі починаємо підставляти похибки останнього відомого шару в \((\text{backprop }2)\) та отримувати нові.

Проінтерпретуймо тепер кожен елемент цього рівняння, щоб воно не здавалося таким страшним і мало якийсь сенс. Отже, знаємо похибки \(\textcolor{darkcyan}{\boldsymbol{\delta}}^{l+1}\) наступного шару, хочемо просунутися на шар назад, тобто порахувати \(\textcolor{darkcyan}{\boldsymbol{\delta}}^l\). Застосовуючи перевернуту певним чином (транспоновану) матрицю вагів \(\left(\textcolor{coral}{W}^{l+1}\right)^\top\), ми ніби просуваємося в зворотному порядку за лінійними зв'язками (коли ми просуваємося в прямому порядку й рахуємо відповідь мережі, застосовуємо просто \(\textcolor{coral}{W}^{l+1}\)). Домножуючи потім на похідну функції активації \(\textcolor{mediumseagreen}{\boldsymbol{\sigma}\textcolor{black}{'}(\textcolor{indianred}{\boldsymbol{p}} \textcolor{black}{^l})}\), ми просуваємо похибку ще трохи назад, на момент до застосування функції активації (див. малюнок 3). Знову таки, більш строгі доведення будуть пізніше.

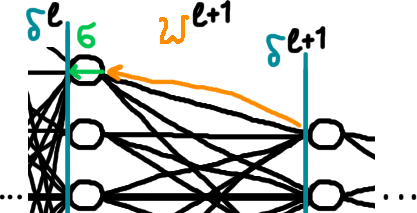
Рівняння зміни функції \(\textcolor{darkcyan}{L}\) втрат відносно довільного параметру зміщення \(\textcolor{steelblue}{b}^l_j\) в мережі. \[ \frac{\partial \textcolor{darkcyan}{L}}{\partial \textcolor{steelblue}{b}^l_j} = \textcolor{darkcyan}{\delta}^l_j \tag{backprop 3} \] У нашій мережі, як ви пам'ятаєте, присутні два типи параметрів: множники \(\textcolor{coral}{W}^l\) та доданки \(\textcolor{steelblue}{\boldsymbol{b}}^l\). Саме ці параметри ми будемо змінювати, бо в цьому сенс машинного навчання. Ми навчилися просуватися вглиб мережі й рахувати значення якоїсь введеної нами величини \(\textcolor{darkcyan}{\delta}\), та це не має жодного сенсу якщо ми не можемо обчислити, в який бік змінювати окремі параметри мережі, тобто не можемо порахувати похідні від функції втрат за цими параметрами. Так от, ми можемо. Наприклад зміна фукнції втрат відносно параметрів-доданків буквально дорівнює похибці \(\textcolor{darkcyan}{\delta}\) на цьому шарі мережі.

Рівняння зміни функції \(\textcolor{darkcyan}{L}\) втрат відносно довільного параметру ваги \(\textcolor{coral}{w}^l_{jk}\) в мережі. \[ \frac{\partial \textcolor{darkcyan}{L}}{\partial \textcolor{coral}{w}^l_{jk}} = \textcolor{firebrick}{a}^{l-1}_k\textcolor{darkcyan}{\delta}^l_j \tag{backprop 4} \] де \(\textcolor{firebrick}{a}^{l-1}_k\) — активований сигнал нейрону попереднього шару; \(\textcolor{darkcyan}{\delta}^l_j\) — похибка нейронів наступного шару (див. малюнок 4). Формула може виглядати трохи заплутано, через те, що параметри-множники знаходяться МІЖ шарами нейронів, тобто нагадаю, що \(\textcolor{coral}{w}^l_{jk}\) — це коєфіцієнт при сполученні \(k\)-того нейрону \((l-1)\)-го шару з \(j\)-тим нейроном \(l\)-того шару.

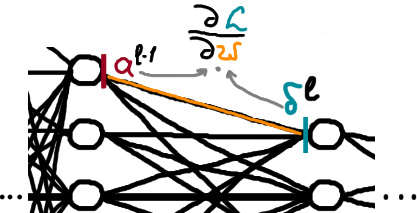
Таким чином, ми навчилися просуватися з останнього шару до попередніх, використовуючи відомі нам величини, та встановили відповідність між величинами в \((4)\), що дає змогу оптимізувати модель без зайвих розрахунків.

Накреси доведень

Не буду брехати, чітких доведень усіх тверджень тут не буде, хоча вони не дуже важкі й цілком зрозумілі. Я опишу, на що саме треба спиратися, але залишу це як завдання читачеві, адже так буде більше користі. Іще зауваження: у цій секції статті я посилаюся на правило похідної композиції функцій та використовую знак суми \(\sum\), якого уникав увесь час, щоб не злякати зайвий раз початківців.

Отже, для всіх рівнянь крім другого робимо таке: пригадуємо, як ми визначили \(\textcolor{darkcyan}{\delta}^l_j\), а також правило диференціювання композиції функцій (chain rule або ланцюгове правило). Власне, доведення у вас прямо в кишені, просто розписуєте відповідні величини як похідні композицій від функцій.

Друге рівняння \((\text{backprop }2)\) розберемо на прикладі, адже воно трохи складніше (на мій погляд). Це рівняння, нагадаю, задає \(\textcolor{darkcyan}{\boldsymbol{\delta}}^l\) в термінах \(\textcolor{darkcyan}{\boldsymbol{\delta}}^{l+1}\).

Розпишімо \(\textcolor{darkcyan}{\delta}^l_j = \partial \textcolor{darkcyan}{L} / \partial \textcolor{indianred}{p}^l_j\) в термінах \(\textcolor{darkcyan}{\delta}^{l+1}_j = \partial \textcolor{darkcyan}{L} / \partial \textcolor{indianred}{p}^{l+1}_j\) за правилом ланцюга: \[ \begin{eqnarray} \textcolor{darkcyan}{\delta}^l_j & = & \frac{\partial \textcolor{darkcyan}{L}}{ \partial \textcolor{indianred}{p}^l_j} = \\ & &\text{| правило ланцюга |} \\ & = & \sum_\textcolor{sienna}{k} \frac{\partial \textcolor{darkcyan}{L}}{ \partial \textcolor{indianred}{p}^{l+1}_\textcolor{sienna}{k}} \frac{\partial \textcolor{indianred}{p}^{l+1}_\textcolor{sienna}{k}}{ \partial \textcolor{indianred}{p}^l_j} = \\ & = & \sum_\textcolor{sienna}{k} \textcolor{darkcyan}{\delta}^{l+1}_\textcolor{sienna}{k} \frac{\partial \textcolor{indianred}{p}^{l+1}_\textcolor{sienna}{k}}{ \partial \textcolor{indianred}{p}^l_j}, \tag{6} \end{eqnarray}\] Залишається порахувати \({\partial \textcolor{indianred}{p}^{l+1}_\textcolor{sienna}{k}}/{ \partial \textcolor{indianred}{p}^l_j}\): \[ \begin{eqnarray} \frac{\partial}{ \partial \textcolor{indianred}{p}^l_j} \textcolor{indianred}{p}^{l+1}_\textcolor{sienna}{k} & = &\frac{\partial}{ \partial \textcolor{indianred}{p}^l_j} \left( \sum_i \textcolor{coral}{w}^{l+1}_{\textcolor{sienna}{k}i}\textcolor{firebrick}{a}^l_i +\textcolor{steelblue}{b}^{l+1}_\textcolor{sienna}{k} \right) =\\ & & \text{| з (1.1) випливає |}\\ & = & \frac{\partial}{ \partial \textcolor{indianred}{p}^l_j} \left( \sum_i \textcolor{coral}{w}^{l+1}_{\textcolor{sienna}{k}i}\textcolor{mediumseagreen}{\sigma(\textcolor{indianred}{p}\textcolor{black}{^l_i})} +\textcolor{steelblue}{b}^{l+1}_\textcolor{sienna}{k} \right) = \\ & & \text{| усі крім j-го доданки суми не залежать від }\textcolor{indianred}{p}^l_j\text{, тому зникають |}\\ & = & \textcolor{coral}{w}^{l+1}_{\textcolor{sienna}{k}j}\textcolor{mediumseagreen}{\sigma\textcolor{black}{'}(\textcolor{indianred}{p}\textcolor{black}{^l_j})}, \tag{7} \end{eqnarray}\] Тоді підставимо \((7)\) у \((6)\): \[ \textcolor{darkcyan}{\delta}^l_j = \sum_\textcolor{sienna}{k} \textcolor{darkcyan}{\delta}^{l+1}_\textcolor{sienna}{k} \textcolor{coral}{w}^{l+1}_{\textcolor{sienna}{k}j}\textcolor{mediumseagreen}{\sigma\textcolor{black}{'}(\textcolor{indianred}{p}\textcolor{black}{^l_j})}. \tag{8}\] Що є рівно тим самим \((\text{backprop }2)\), але в поелементному вигляді.

Алгоритм

Сформулюймо тепер чіткий алгоритм зворотного поширення помилки (backprop).

1. Вхідні дані: подаємо вхідні данні \(x\) у модель, вважаємо що це значення найперших нейронів.
2. Прямий прохід: рахуємо, як зазвичай, значення всіх шарів нейронної мережі поступово, отримаємо всі \(\textcolor{indianred}{p}^l_j\) та \(\textcolor{firebrick}{a}^l_j = \textcolor{mediumseagreen}{\sigma(}\textcolor{indianred}{p}^l_j \textcolor{mediumseagreen}{)}\). Ці значення використовуватимуться в зворотному поширенні, але вони потрібні на цьому кроці для обрахування передбачення моделі (значення на останньому шарі), тобто будуть уже обраховані.
3. Помилка на виході: рахуємо, наскільки модель помилилася, тобто функцію втрат, тобто як відрізняються значення \(\textcolor{firebrick}{\boldsymbol{a}}^N\) на останньому шарі нейронів від того, що ми вважали б правдою, \(\boldsymbol{y}\). Також рахуємо похибку \(\textcolor{darkcyan}{\boldsymbol{\delta}}^N = \left( \nabla_{\textcolor{firebrick}{a}^N} \textcolor{darkcyan}{L} \right) \odot \left( \textcolor{mediumseagreen}{\boldsymbol{\sigma}\textcolor{black}{'}(\textcolor{indianred}{\boldsymbol{p}} \textcolor{black}{^N})} \right)\).
4. Поширити помилку назад: починаючи з передостаннього шару \(l=N-1\), рахуємо \(\textcolor{darkcyan}{\boldsymbol{\delta}}^l = \left( \left(\textcolor{coral}{W}^{l+1}\right)^\top \textcolor{darkcyan}{\boldsymbol{\delta}}^{l+1} \right) \odot \left( \textcolor{mediumseagreen}{\boldsymbol{\sigma}\textcolor{black}{'}(\textcolor{indianred}{\boldsymbol{p}} \textcolor{black}{^l})} \right)\) для всіх попередніх шарів.
5. Результат алгоритму: за допомогою похибок нейронів кожного шару, рахуємо відповідні частинні похідні від функції втрат за всіма параметрами \({\partial \textcolor{darkcyan}{L}}/{\partial \textcolor{steelblue}{b}^l_j} = \textcolor{darkcyan}{\delta}^l_j\) та \({\partial \textcolor{darkcyan}{L}}/{\partial \textcolor{coral}{w}^l_{jk}} = \textcolor{firebrick}{a}^{l-1}_k\textcolor{darkcyan}{\delta}^l_j\), звідки отримуємо градієнт функції втрат за параметрами, який уже можна використати для навчання градієнтним спуском.

Для ілюстрації ще раз наведу малюнок 2:

Підсумки й спрощена інтерпретація

Отже, повторімо загалом, про що алгоритм, перефразовуючи його сутність, щоб дати альтернативні способи розуміння. У тренуванні моделей (тобто підборі параметрів для них) ми хочемо змінювати параметри поступово так, аби модель краще відображала наш набір даних. Будемо проходити наш тренувальний набір, усі його окремі приклади, рахуючи, наскільки помиляється модель у поточному стані на цих прикладах. Порахувавши нашу помилку \(\textcolor{darkcyan}{L}\), щоб установити, як саме змінювати кожен із параметрів, ми почнемо розповсюджувати, ніби розмазувати, цю величину помилки \(\textcolor{darkcyan}{L}\) по всіх нейронах і по кожному з параметрів цього нейрона поступово назад. На це можна дивитися так: у нас є загальна характеристика того, як модель помиляється, \(\textcolor{darkcyan}{L}\), і ми намагаємося встановити, наскільки нам звинувачувати в цій помилці кожен окремий параметр. Якщо параметр справді винний у певній частині цієї помилки, ми його змінюємо (збільшуємо/зменшіємо залежно від знаку похідної), але якщо він мало впливає на помилку, то його сильно чіпати не будемо. Щоб установити "степінь провини" кожного окремого параметру, ми починаємо з загальної помилки \(\textcolor{darkcyan}{L}\), потім рахуємо, наскільки винний кожен окремий нейрон останнього шару, тобто шару, що напряму впливає на відповіді, (це рівняння \((\text{backprop }1)\)). Далі, за допомогою \((\text{backprop }2)\) ми можемо продовжувати розмазувати провину на нейрони попереднього шару за схожою логікою: якщо нейрон останнього шару помилився на \(\textcolor{darkcyan}{\delta}^N\), то можна встановити, наскільки цьому посприяли нейрони попереднього шару, за рахунок яких він і формує свій сигнал. Таким чином рахуємо "степінь провини" для нейронів попереднього шару. Далі рівняння\((\text{backprop }3-4)\) показують, як "степінь провини" нейрону дає розуміння про те, наскільки помилилися окремі параметри йього нейрону. Ну й маючи вже цю інформацію, можемо зробити висновки для кожного з параметрів щодо зміни його значення на краще.

Завдання

Пропоную деякі завдання для кращого розуміння матеріялу статті. Їх відсортовано за зростанням складности.

   1. Перечитати незрозумілі частини статті та намагатися їх інтерпретувати. Перечитати інтуїтивні пояснення в статті. Як-то кажуть, it takes some time, на це треба час.

   2. Який вигляд матимуть рівняння зворотного поширення помилки у випадку мережі, де немає функції активації? Інакше кажучи, треба встановити, як працює backprop у випадку \(\textcolor{mediumseagreen}{\sigma(\textcolor{black}{x})} \equiv x\) (підставити в наші загальні рівняння), коли \(\textcolor{mediumseagreen}{\sigma(\textcolor{black}{\cdot})}\) нічого не змінює. Це непрактичний випадок, який не матиме багато застосувань, але його іноді розглядають у теорії для пояснень роботи методів машинного навчання.

   3. Передивіться секцію з накресами доведень та спробуйте довести рівняння \((\text{backprop }1)\), \((\text{backprop }3)\), \((\text{backprop }4)\).

   4. Запрограмуйте цей алгоритм.